Bloq.III

Introducción

 En bloques anteriores analizamos la importancia del concepto de función, así como sus elementos generales. 

En este bloque analizaremos ahora un grupo particular de funciones llamadas algebraicas y dentro de estas aquellas llamadas polinomiales.

 

Analizaremos las características de las funciones de polinomiales de grado cero(constante), de grado uno(lineal e identidad) y de grado dos (cuadráticas), además de algunos conceptos básicos de relacionados con ellas como el cero o raíz de una función. 

Función polinomial

Una función polinomial es una función  en que f ( x ) es un polinomio en x .

Una función polinomial de grado  n es escrita como  .

Las funciones polinomiales están definidas y son continuas en todos los números reales.

POLINOMIALES DE GRADO BAJO
NOMBRE	FORMA	GRADO
Función constante	f ( x ) = a	0
Función lineal	f ( x ) = ax + b, a ≠ 0	1
Función cuadrática	f ( x ) = ax 2 + bx + c , a ≠ 0	2

Función constante

Una función constante es una función lineal por la cual el rango  no cambia sin importar cual miembro del dominio  es usado.    para cualquier x 1 y x 2 en el dominio.

Con una función constante, para cualesquiera dos puntos en el intervalo, un cambio en x resulta en un cambio en cero en f ( x ).

Ejemplo:

Grafique la función f ( x ) = 3.

   

Encontrar el dominio y rango de una función constante

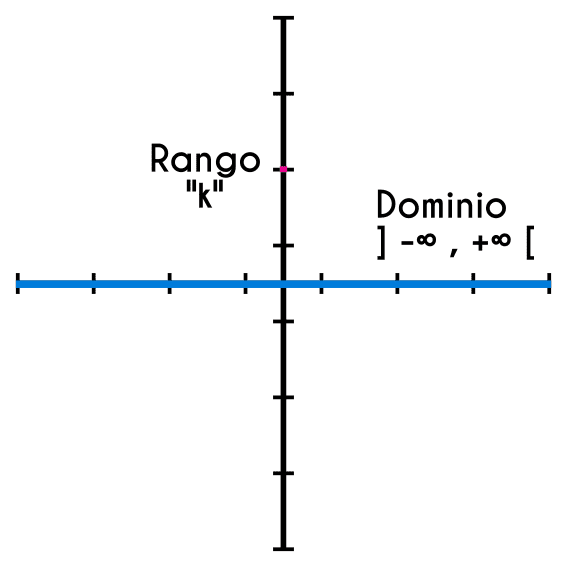
Ejemplos de funciones constantes

Función lineal (primer grado)

Una función lineal es una función cuyo dominio son todos los números reales, cuyo codominio también todos los números reales, y cuya expresión analítica es un polinomio de primer grado.

La función lineal se define por la ecuación f(x) = mx + b ó y = mx + b llamada ecuación canónica, en donde m es la pendiente de la recta y b es el intercepto con el eje Y.

Por ejemplo, son funciones lineales f(x) = 3x + 2 g(x) = - x + 7 h(x) = 4 (en esta m = 0 por lo que 0x no se pone en la ecuación).

Esta es la gráfica de la función lineal y = 3x + 2

Vemos que m = 3 y b = 2 (de la forma y = mx + b)

Este número m se llama pendiente de la recta y es la relación entre la altura y la base, aquí vemos que por cada unidad recorrida en x la recta sube 3 unidades en y por lo que la pendiente es m = 3. & b es el intercepto de la recta con el eje Y (donde la recta se cruza con el eje Y)

Volvamos al ejemplo de las funciones lineales

f(x) = 3x+2       

                      Si x es 3,  entonces f (3) = 3*3+2 = 11

Si x es 4,  entonces f (4) = 3*4+2 = 14

Si x es 5,  entonces f (5) = 3*5+2 = 17

Cada vez que la x se incrementa en 1 unidad, el resultado, esto es, f(x), se incrementa en 3 unidades. Si el valor de la pendiente es positivo la función es Creciente. Preste atención en que los valores de   x  y de  f(x)  NO SON PROPORCIONALES.

Lo que son proporcionales son los incrementos.

g(x) = -3x+7     

                      Si  x= 0, entonces g (0) = -3*(0) +7 =   0+7 = 7

Si  x= 1, entonces g (1) = -3*(1) +7 = -3+7 = 4

Si  x= 2, entonces g (2) = -3*(2) +7 = -6+7 = 1

Cada vez que la x se incrementa en 1 unidad, el resultado, esto es, g(x), disminuye en 3 unidades. Si el valor de la pendiente es negativo la función es Decreciente.

h(x) = 4            

                     Si  x= 0   ,  entonces h(0)  = 4

Si  x= 98   entonces h(98) = 4

Cada vez que la x se incrementa en 1 unidad, el resultado, esto es, h(x), NO aumenta. Es la función constante. Su gráfica es una recta paralela al eje X.

Esta es la representación grafica de los tres tipos de funciones descritas.

Si quieres ampliar estos conceptos te recomiendo estas paginas:

http://es.wikipedia.org/wiki/Funci%C3%B3n_lineal

http://www.x.edu.uy/lineal.htm

http://www.ing.unp.edu.ar/matematica/Modulos/Unidad_4.PDF

Ejemplos

Representa gráficamente las siguientes funciones lineales  y = 2x  y  y = - 3x + 4

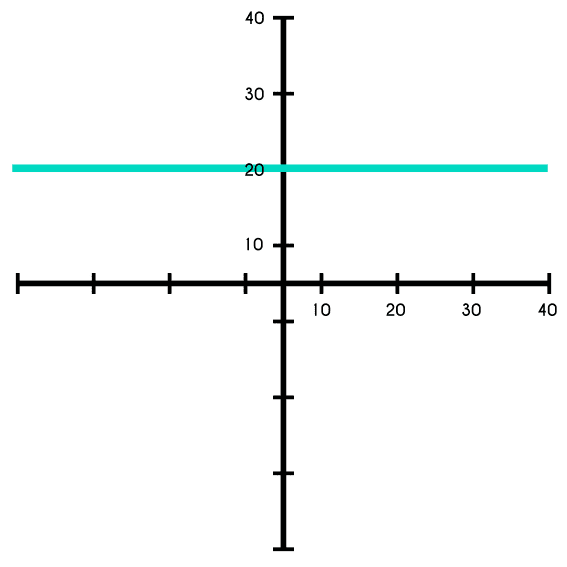
Sugerencia: Primero elabora una tabla de valores, luego ubica los pares de puntos de la tabla en el plano cartesiano y finalmente únelos con una línea recta.

Los valores de x son asignados arbitrariamente o a tu gusto "te aconsejo usar valores pequeños para facilitar las operaciones" luego en la ecuación remplazamos la x por cada valor de la tabla. 

1.       y = 2x
Vamos a hacerlo con dos valores de x para que sepas de donde salen los valores.

       Para x = - 2, y = 2(-2) = -4  quedando la pareja (-2 , -4)

       Para x =  1,  y = 2(1)  =  2   quedando la pareja (1 , 2)

X	y = 2x
-2	-4
-1	-2
0	0
1	2
2	4

2.       y = - 3x + 4
Vamos a hacerlo con dos valores de x para que sepas de donde salen los valores.

       Para x = - 1, y = -3(-1)+ 4 =  7  quedando la pareja (-1 , 7)

       Para x =  2,  y = -3(2) + 4 = -2   quedando la pareja (2 , -2)

X	y = - 3x + 4
-1	7
0	4
1	1
2	-2
3	-5

Si tienes dudas de como graficar una función lineal te recomiendo estos vídeos:

Función cuadrática

La forma general de una función cuadrática es f ( x ) = ax 2 + bx + c . La gráfica de una función cuadrática es una parábola , un tipo de curva de 2 dimensiones.

La parábola "básica", y = x 2 , se ve así:

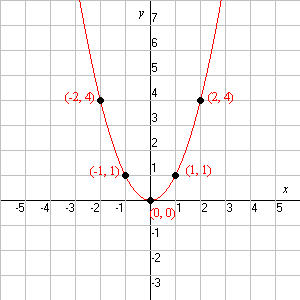
La función del coeficiente a en la ecuación general es de hacer la parábola "más amplia" o "más delgada", o de darle la vuelta (si es negativa):

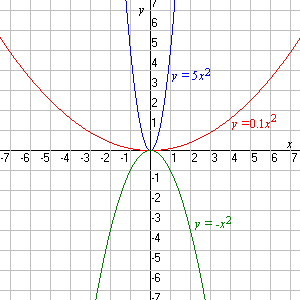
Si el coeficiente de x 2 es positivo, la parábola abre hacia arriba; de otra forma abre hacia abajo.

El vértice

El vértice de una parábola es el punto en la parte baja de la forma "U" (o la superior, si la parábola abre hacia abajo).

La ecuación para una parábola también puede escribirse en la "forma vértice":

y = a ( x – h ) 2 + k

En esta ecuación, el vértice de la parábola es el punto ( h , k ).

Puede ver como esto se relaciona a la ecuación estándar al multiplicarla:

y = a ( x – h )( x – h ) + k

y = ax 2 – 2 ahx + ah 2 + k

El coeficiente de x aquí es – 2 ah . Esto significa que en la forma estándar, y = ax 2 + bx + c , la expresión

nos da la coordenada en x del vértice .

Ejemplo:

Encuentre el vértice de la parábola.

y = 3 x 2 + 12 x – 12

Aquí, a = 3 y b = 12. Así, la coordenada en x del vértice es:

Sustituyendo en la ecuación original para obtener la coordenada en y , obtenemos:

y = 3(–2) 2 + 12(–2) – 12

= –24

Así, el vértice de la parábola esta en ( – 2, – 24).

El eje de simetría

El eje de simetría de una parábola es la recta vertical a través del vértice. Para una parábola en la forma estándar, y = ax 2 + bx + c , el eje de simetría tiene la ecuación

Dese cuenta que – b /2 a es también la coordenada en x del vértice de la parábola.

Ejemplo:

Encuentre el eje de simetría.

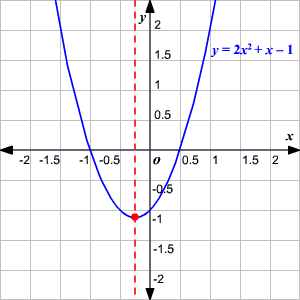
y = 2 x 2 + x – 1

Aquí, a = 2 y b = 1. Así, el el eje de simetría es la recta vertical

Intercepciones

Puede encontrar la intercepción en y de una parábola simplemente al introducir 0 para x . Si la ecuación esta en la forma estándar, entonces Usted solo toma a c como la intercepción en y . Por ejemplo, en el ejemplo anterior:

y = 2(0) 2 + (0) – 1 = –1

Así la intercepción en y es – 1.

Las intercepciones en x son un poco más complicadas. Puede usar la factorización , o completar el cuadrado , o la fórmula cuadrática para encontrar estas (si es que existen!).

Dominio y rango

Como con cualquier función, el dominio de función cuadrática f ( x ) es el conjunto de los valores de x para los cuales la función esta definida, y el rango es el conjunto de todos los valores de salida (valores de f ).

Las funciones cuadráticas generalmente tienen la recta real de enteros como su dominio: cualquier x es una entrada legítima. El rango esta restringido a esos puntos mayores que o iguales a la coordenada en y del vértice (o menores que o iguales a, dependiendo si la parábola abre hacia arriba o hacia abajo).

Si tienes dudas de como graficar una función cuadratica te recomiendo estos vídeos: