Concepto de función
Se denomina una función a una relación entre un conjunto A y un conjunto B donde cada dato del conjunto A puede tomar solamente un valor del conjunto B. Aunque el conjunto A solo puede tomar un solo valor del conjunto B, un elemento del conjunto B si puede tomar estar relacionado con 2 o más elementos del conjunto A. Aunque esto puede parecer un poco complicado, al final el tema de la funciones trata en encontrar una relación entre dos conjuntos de datos, como podría ser una relación entre la distancia que un ser humano avanza caminando con respecto al tiempo o cualquier otro tipo de relación entre 2 conjuntos de valores.
Para comprender un poco mejor el concepto general de una función se tomará el siguiente ejemplo.
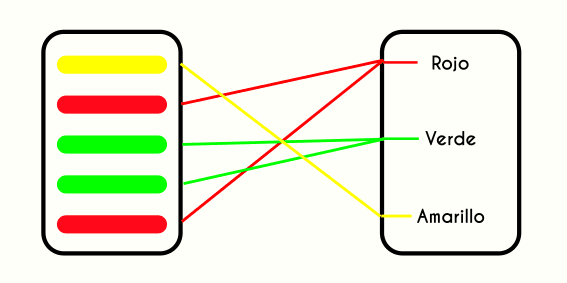
Explicación de la imagen
Como se puede observar en la imagen anterior hay dos conjuntos, los elementos que componen al conjunto de la derecha son nombres de colores, mientras que los elementos de la izquierda son cuadros de diferentes colores, como se puede observar cada nombre de color se relaciona con cada cuadro que tiene ese mismo color, porque hay mas de un cuadro que repite color con otro, sin embargo en el conjunto de la izquierda (que son los cuadros de colores) solamente toman un nombre del color, porque el color azul no puede ser azul y rosado a la vez, por lo que se cumple el concepto de que “el conjunto B puede estar relacionado solamente con un elemento del conjunto A” donde “A” son los nombres de los colores y “B” son los cuadros de colores.
Funciones matemáticas
Lo anterior era solamente para el concepto básico de una función, en realidad una función se mira tal que así: f(x) = 4x + 1. Una función es simplemente una ecuación con una variable, por lo general la incógnita es representada por la letra “x” aunque se puede utilizar cualquier letra del abecedario y al lado izquierdo de la ecuación está escrito “f(x)” que se lee “f de x” aunque también se puede escribir como una variable “y” ( f(x) = y ).
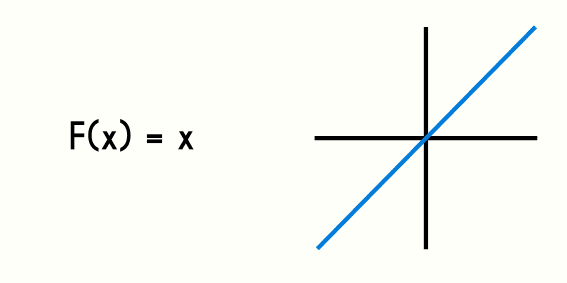
Evaluar una función matemática
Una función matemática consta de una variable dependiente y de una variable independiente, para explicar esto se tomará el siguiente ejemplo.
Se tomará la función f(x) = 2x, para ver como se va desarrollando una función lo que se hace es ir “evaluando la función” en diferentes valores, esto se hace cambiando la variable “x” por valores numericos
Por ejemplo: cuando x toma el valor de 0 entonces se hace lo siguiente:
Como se puede ver se cambia la variable “x” en ambos lados de la función por el valor x (en este caso es 0) y se resuelve la ecuacion, en este caso el resultado fue cero, y esta es la manera de evaluar una función, por ejemplo para evaluar f(x) = 2x, en los valores 1, 2, y 3 se hace el mismo procedimiento.
Como se puede observar en el ejemplo anterior la variable independiente de una función siempre será “x” y la variable dependiente de la función será “f(x) o y”, esto se define así porque dependiendo del valor que tome “x” así será el cambio de “y”.
Otra forma de ver a una función es imaginarla como un sistema, donde podremos introducir un número cualquiera y este sistema nos arroja una respuesta, tal y como se puede observar en la siguiente ilistración.
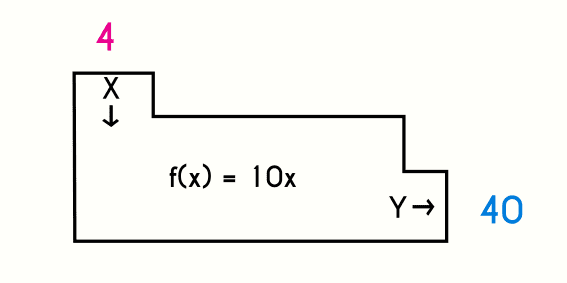
Grafica de una función matemática
Una gran parte del tema de las funciones son sus graficas, porque dependiendo del tipo de función que sea así será su grafica, para graficar cualquier función, una de las formas más practicas de hacerlo es evaluando la función en ciertos valores de “x” y tomar los resultados de “y”, de esta manera se tendrán las coordenadas por donde pasa la función, y luego solo se unen cada una de los puntos en un plano cartesiano y ya se tendría la grafica de cualquier función.
Al igual que con el dominio y el rango hay procesos que permiten graficar una función de manera más directa simplemente usando la ecuación de la función.
Para demostrar como graficar una función se realizará el siguiente ejemplo: graficar la función f(x) = x2
Primero se hará una tabla donde se escribirá en la columna izquierda los valores en los que se va a evaluar la función, en la columna central la ecuación con cada valor de “x” y en la columna de la derecha se pondrá el resultado, y con esto ya se habrán encontrado las coordenadas por donde pasa la función.
| x | f(x) = x2 | y |
|---|---|---|
| -2 | f(-2) = -22 | 4 |
| -1 | f(-1) = -12 | 1 |
| 0 | f(0) = 02 | 0 |
| 1 | f(1) = 12 | 1 |
| 2 | f(2) = 22 | 4 |
Ahora se ubican las coordenadas en un plano cartesiano y se unen con una linea.
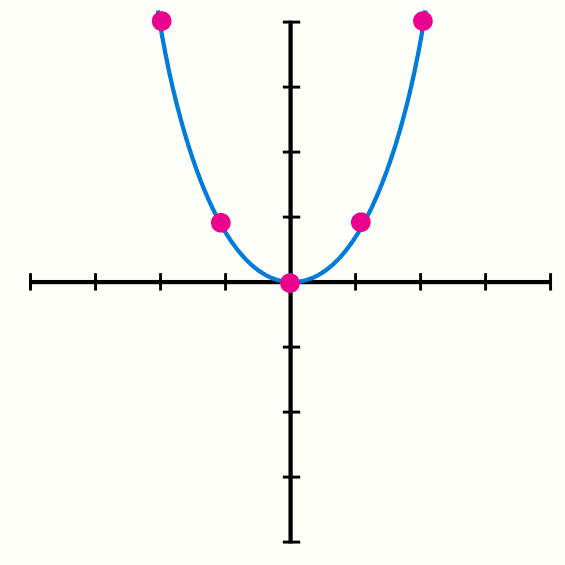
Como se puede observar en este caso al ser una función de segundo grado la grafica tiene una forma de parábola.
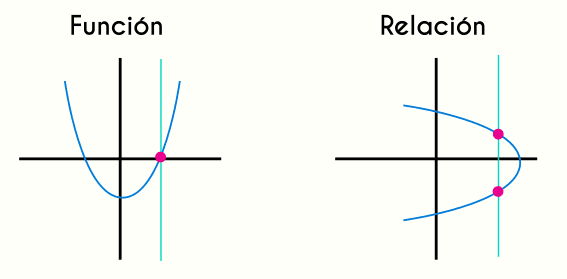
Una característica de las graficas de las funciones es que si se traza una linea recta vertical, solamente puede cortar una ves con la función, de lo contrario esta no es una función sino una relación, esto se debe al concepto de funciones que se definió en el inicio de este articulo, y es que el dominio solamente puede tomar un valor del rango.
Conjunto A alumnos del salón de clases y el conjunto P es un subconjunto del peso de cada
estudiante:
Una relación de un conjunto X en un conjunto Y que satisfaga esta
condición se llama función y la definimos como función y la definimos como:
Una función f de un conjunto X en un conjunto Y es una relación entre estos que cumple la condición de que cada elemento de X está relacionado con uno y solamente uno de Y.
Observe que la función se denota f(x) y generalmente es igual a y
Una regla de asociación se
puede escribir como función o viceversa. ejemplos:
1.- Si la regla de asociación es “el cuadrado de un número más tres”, entonces la función que la representa es:
Establece la regla de
asociación entre los siguientes conjuntos de números:
1.-
A = {-2,-1,-0,1,2,3} B= {-10,-5,0,5,10,15}
2.- C = {-10,-8,-6,-4,-2,0,2,4,6,8,10} D= {-5,-4,-3,-2,-1,0,1,2,3,4,5}
3.-
E = {-3,-2,-1,0,1,2,3,} F= {27,-8,-1,0,1,8,27}
4 .- G = {-3,-2,-1,-0,1,2,3} H=
{-30,-11,-4,-3,-2,5,24}
5.-
I = {-2,-1,-0,1,2,3} J= {-10,-5,0,5,10,15}
Identifica cuales de las siguientes relaciones son funciones
Dominio y rango de una función
El dominio y rango de una función define que tan lejos llega una función en cuestión de números, se define como dominio a todos los valores de “x” que son validos en la función y se toma como rango de la función (en ocasiones también conocido como imagen de la función) a todo valor de “y” que sea parte de la función.
Recordatorio: Los números reales son el conjunto de números que contienen los números enteros positivos, los enteros negativos y los decimales.
Qué es el dominio de una función
Dominio de una función: Cuando se habla de un valor valido de “x” se refiere a que el valor que tome “x” en un momento determinado de como resultado una respuesta que se pueda representar en los números reales, por ejemplo en la siguiente función: f(x) = 2x, no importa que valor tome la variable “x”, ya sea extremadamente alto o extremadamente bajo, el resultado siempre podrá ser representado en los números reales, en casos como el anterior que acepta todos los números de “x” se define que el dominio de la función son todos los reales.
El dominio de la función anterior se puede escribir en intervalos de la siguiente manera ]- ∞ , +∞[ que se lee: desde menos infinito hasta mas infinito.
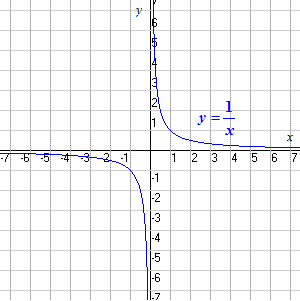
El dominio de una función matemática deja de ser los reales cuando “x” toma un valor que no es aceptado en la ecuación de la función, por ejemplo en la función f(x) = 1/x, tanto en x=1, como en x=-1 la función tiene una respuesta valida, pero cuando x toma el valor de 0, entonces este procedimiento no se puede resolver, porque entonces se estaría dividiendo entre cero y no se puede dividir ningún número entre cero (al menos hasta ahora), por lo que en esta función el dominio de la función no son los números reales, porque 0 es parte de los reales y este no forma parte del dominio.
Qué es el rango de una función
Rango de una función: el rango de una función se conforma por todos los resultados que f(x) toma a lo largo de evaluar una función en todos los números, el rango de una función va a depender mucho de los tipos de funciones que sean.
En la función f(x) = 4x, el rango son los reales, porque mientras mas crece el valor de “x” mas crece el rango de la función y también viceversa, mientras mas decrecen los valores de “x” mas decrece el rango hasta llegar a infinito en ambos lados.
Una función donde se puede comprobar que hay rangos que no llegán hasta infinito es en la función seno f(x) = sen(x), aquí el rango solo va desde -1 hasta 1, es decir que la amplitud del rango de la función es de 2, se puede comprobar esto evaluando la función en diferentes valores de “x” y no importa que tan grande sea el valor de x el resultado siempre dará un numero entre -1 y 1.
El dominio y rango depende del tipo de función
Definir el dominio y rango de una función evaluando la función es prácticamente imposible, por eso cada tipo de función tiene una forma diferente de poder definir el dominio y rango de la función en ocasiones basta con mirar la ecuación para darse cuenta como es el dominio y rango mientras que en otras ocasiones se requiere de unos cuantos pasos mas para poder definirlos.
Ejemplo 1:
Considere la función mostrada en el diagrama.

Aquí, el dominio es el conjunto { A , B , C , E }. D no está en el dominio, ya que la función no está definida para D .
El rango es el conjunto {1, 3, 4}. 2 no está en el rango, ya que no hay letra en el dominio que se enlace con el 2
Ejemplo 2:
El dominio de la función
f ( x ) = 1/ x
es todos los números reales excepto el cero (ya que en x = 0, la función no está definida: la división entre cero no está permitida!).
El rango también es todos los números reales excepto el cero. Puede ver que hay algún punto en la curva para cada valor de y excepto para y = 0.
Ejemplo 3:
La notación siguiente muestra que el dominio de la función está restringido al intervalo (–1, 1).
f ( x ) = x 2 , –1  x
x  1
1
La gráfica de esta función es como se muestra. Dese cuenta de los círculos abiertos, que muestran que la función no está definida en x = –1 y x = 1. Los valores del rango de y desde 0 hasta el 1 (incluyendo el 0, pero no incluyendo el 1). Así el rango de la función es
0  y < 1.
y < 1.

Dominio y rango de una Función








No hay comentarios:
Publicar un comentario