Funciones inversas
Las funciones f y g son funciones inversas si f ( g ( x )) = x para todas las x en el dominio de g y g ( f ( x )) = x para todas las x en el dominio de f .
La inversa de una función f es usualmente denotada por f –1 y se lee “ f inversa.” (Dese cuenta que el superíndice –1 en f –1 no es un exponente).
Suponga que dos funciones son inversas. Si ( a , b ) es un punto en la gráfica de la función original, entonces el punto ( b, a ) debe ser un punto en la gráfica de la función inversa. Las gráficas son imágenes espejo una de otra con respecto a la recta y = x .

Para encontrar la inversa de una función algebraicamente, intercambie la x y la y y resuelva para y .
Ejemplo:
Digamos que h ( x ) = x 3 + 4
Reemplace h ( x ) con y e intercambie x y y :
y = x 3 + 4
x = y 3 + 4
Resuelva para y : x – 4 = y 3

Funciones de valor absoluto
Una función de valor absoluto es una función que contiene una expresión algebraica dentro de los símbolos de valor absoluto. Recuerde que el valor absoluto de un número es su distancia desde 0 en la recta numérica.
La función padre de valor absoluto, escrita como f ( x ) = | x |, está definida como

Para graficar una función de valor absoluto, escoja diferentes valores de x y encuentre algunas parejas ordenadas.

Grafique los puntos en una plano coordenado y unálos.

Observe que la gráfica es de la forma V.
(1) El vértice de la gráfica es (0, 0).
(2) El eje simetría ( x = 0 o eje de las y ) es la recta que divide la gráfica en dos mitades congruentes.
(3) El dominio es el conjunto de todos los números reales.
4) El rango es el conjunto de todos los números reales mayores que o iguales a 0.  .
.
(5) La intercepción en x y la intercepción en y ambas son 0.
Cambio Vertical
Para trasladar la función valor absoluto f ( x ) = | x | verticalmente, puede utilizar la función
g ( x ) = f ( x ) + k .
Donde k > 0, la gráfica de g ( x ) se traslada k unidades hacia arriba.

Donde k < 0, la gráfica de g ( x ) se traslada k unidades hacia abajo.

Cambio Horizontal
Para trasladar la función valor absoluto f ( x ) = | x | horizontalmente, puede utilizar la función
g ( x ) = f ( x + k ).
Donde k > 0, la gráfica de g ( x ) se traslada k unidades a la izquierda.

Donde k < 0, la gráfica de g ( x ) traslada k unidades a la derecha.

Función escalonada
La función escalonada y = s(x) es una función definida a trozos o por partes, tal que en un intervalo finito [a,b] tiene un número finito de discontinuidades, a las cuales llamaremos x0 < x1 < x2 <…. xn. En cada intervalo abierto (xi , xi+1), y tiene un valor constante de valor si, con discontinuidades -saltos- en los puntos xi.
La grafica que resulta de una función como esta consiste en escalones o peldaños. Veamos un ejemplo a continuación:
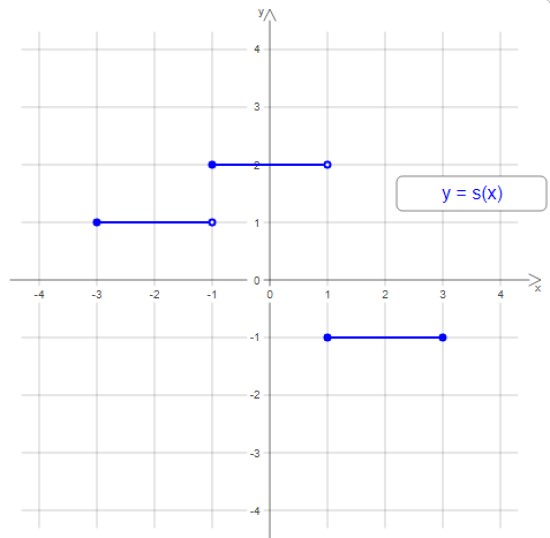
La gráfica de esta función escalonada tiene tres peldaños o intervalos escalonados, pero en general la función escalonada puede tener cualquier cantidad de escalones. La anchura de los escalones puede ser diferente y no siempre la escalera es ascendente o descendente.
La función escalonada del ejemplo se puede escribir especificando el ancho y el alto de cada escalón, así:
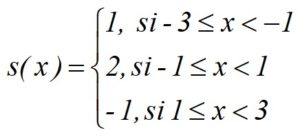
Características de la función escalonada
-La función recibe su nombre por la gráfica en forma de escalones, dados por los segmentos que la componen. Cada segmento tiene una parte del dominio de la función y en cada uno, la función es constante.
-El dominio de una función escalonada son los valores que pertenecen al intervalo para el cual se la define: [a,b], mientras que el rango lo constituyen los valores si de las alturas de los escalones.
En el ejemplo de la figura 1, el dominio es el intervalo [-3,3] y el rango son los valores -1, 1 y 2.
-La función escalonada es continua excepto en los valores que delimitan cada escalón, los puntos xi.
-Las funciones escalonadas se pueden sumar y multiplicar para dar lugar a nuevas funciones escalonadas.
-Su derivada es 0 para los puntos donde está definida, ya que en ellos la función es constante. Por su parte, la derivada no existe en las discontinuidades.
– Ejemplo 1
En una ciudad la tarifa de taxis es de 3.65 $ de base, por los primeros 100 m. Y por cada 100 m son 0.18 $, siendo el límite por recorrido de 50 km.
Se desea establecer la función que relacione el recorrido en metros con el costo del servicio en $, la cual debe tener esta forma:
f (x) = 3.65 + 0.18. [[x /100]] $
Donde la función parte entera puede ser de tipo función cielo, a la cual se añade la tarifa de base que son 3.65 $. Por ejemplo, si queremos saber cuánto se pagará por un viaje de 6.25 km = 6250 m, tendremos:
f (x) = 3.65 + 0.18. [[x /100]] $ = 3.65 + 0.18 . [[6250/100]] $ = 3.65 + [[11.25 ]] $ = 15.65 $
Si la compañía de taxis escoge una función piso, entonces el cliente pagaría un poco menos por el viaje:
f (x) = 3.65 + 0.18. [[x /100]] $ = 3.65 + 0.18 . [[6250/100]] $ = 3.65 + [[11.25 ]] $ = 14.65 $
Ejercicios resueltos
– Ejercicio 1
Las llamadas de larga distancia entre las ciudades A y B cuestan 0.40 $ los primeros 10 minutos. Después de ese lapso, la fracción o minuto adicional vale 0.05 $.
Expresar el costo C (t) de una llamada que dure determinada cantidad de minutos.
Solución
Podemos expresar esta función si vamos analizando lo que sucede con cada opción para la duración de una llamada:
Para t ≤ 10 minutos
Cuando t, que es el tiempo que dure la llamada, sea menor o igual a 10 minutos, se pagan 0.40 $.
Por lo tanto:
f (t) = 0.40 $ para t comprendido entre 0 y 10 minutos.
Ya tenemos una parte de la función.
Para t > 10 minutos
Caso t entero
Ahora veamos lo que sucede cuando se excede el tiempo de t = 10 minutos: puede pasar que el exceso sea un número entero, por ejemplo que la conversación dure exactamente 11, 12, 13, 14 minutos o más. En ese caso el monto de la llamada será:
f (t) = 0.40 + 0.05(t-10) $, para t mayor que 10 minutos, con t entero.
Es decir que en este caso: t = 11, 12, 13, 14, 15 … minutos.
Por ejemplo, supongamos que la conversación dura exactamente 15 minutos, el costo será:
f (15) = 0.40 + 0.05(15-10) $ = 0.65 $
Caso t decimal
Por último, consideremos el caso en que la llamada dure un tiempo con parte decimal. Por ejemplo, supongamos que la llamada dure 15 minutos y 45 segundos, que en forma decimal sería 15.75 minutos.
Lo podemos expresar en términos de la función parte entera del tipo piso, suponiendo que la compañía quiere darle más beneficios al cliente, o de tipo cielo:
f (t) = 0.40 + 0.05 ⋅ [[t-9]] $
Veamos lo que el cliente pagaría si fuera una función piso:
f (15.75) = 0.40 + 0.05 ⋅ [[15.75-9]] $ = 0.40 + 0.05⋅[[6.75]] $ = 0.40 + 0.05× 6 $ = 0.70 $.
O como función cielo, en tal caso el costo sería:
f (15.75) = 0.40 + 0.05 [[15.75-9]] $ = 0.40 + 0.05⋅[[6.75]] $ = 0.40 + 0.05×7 $ = 0.75 $.
Función y gráfica
Como una función definida por partes queda:
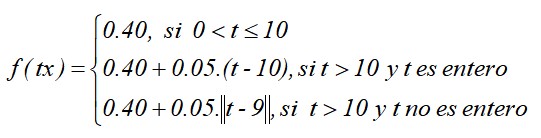
La gráfica de la función quedaría así, suponiendo que se escogió la función parte entera de tipo techo:
Función lineal
Una función lineal es una función que puede ser escrita en la forma f ( x ) = mx + b donde m y b son números reales y m ≠ 0.
Ejemplo:
Grafique la función f ( x ) = 2 x – 1.

La gráfica siempre es una recta con pendiente ya sea positiva o negativa.
Función constante
Una función constante es una función lineal por la cual el rango no cambia sin importar cual miembro del dominio es usado.  para cualquier x 1 y x 2 en el dominio.
para cualquier x 1 y x 2 en el dominio.
Con una función constante, para cualesquiera dos puntos en el intervalo, un cambio en x resulta en un cambio en cero en f ( x ).
Ejemplo:
Grafique la función f ( x ) = 3.

La gráfica de una función constante es siempre una recta horizontal.
función identidad

No hay comentarios:
Publicar un comentario